A* Algorithm

Many computer scientists would agree that A* is the most popular choice for pathfinding, because it’s fairly flexible and can be used in a wide range of contexts. A* is like Dijkstra’s algorithm in that it can be used to find a shortest path. A* is like Greedy Best-First-Search in that it can use a heuristic to guide itself. So what is the relevance of these sort of searching algorithms today? Well, for one they are essential to game artificial intelligence. The notion of pathfinding, or finding a path from ‘A’ to ‘B’, past any obstacles that get in the way, is going to be key in many games. One way to do this is to use the A* algorithm. A* is commonly used for the common pathfinding problem in applications such as games, but was originally designed as a general graph traversal algorithm. It finds applications to diverse problems, including the problem of parsing using stochastic grammars in NLP. Other cases include an Informational search with online learning

Suggested Video

Challenge

#1 Create your own code to illustrate the functionality of this algorithm

#2 Comment each line of the python solution below to show your understanding of the algorithm

Solution - A* Graph Search Algorithm

def A*-GRAPH-SEARCH (start):
  Let pq be an empty min priority queue
  Let closed be an empty set
  
  g(start) = 0
  f(start) = h(start)
  path(start) = []
  pq.push(start, f(start))
  
  while not pq.empty():
    top = pq.pop()
    if isGoal(top):
      return f(top), path(top)
    closed.add(top)
    foreach next in succ(top):
      if next not in closed:
        g(next) = g(top) + cost(top, next)
        f(next) = g(next) + h(next)
        path(next) = path(top).append(next)
        pq.push(next, f(next))

Solution - A* Tree Search Algorithm

def A*-TREE-SEARCH (start):
  Let pq be an empty min priority queue
  
  g(start) = 0
  f(start) = h(start)
  path(start) = []
  pq.push(start, f(start))
  
  while not pq.empty():
    top = pq.pop()
    if isGoal(top):
      return f(top), path(top)
    foreach next in succ(top):
      g(next) = g(top) + cost(top, next)
      f(next) = g(next) + h(next)
      path(next) = path(top).append(next)
      pq.push(next, f(next))

The above two examples are taken from: https:// kartikkukreja. wordpress. com

Additional A* Algorithm Implementation example from:

https://gist.github.com/jamiees2/5531924

Wiki animations and illustrations

#1: A* was invented by researchers working on Shakey the Robot's path planning.

---

#2: Illustration of A* search for finding path from a start node to a goal node in a robot motion planning problem. The empty circles represent the nodes in the open set, i.e., those that remain to be explored, and the filled ones are in the closed set. Color on each closed node indicates the distance from the start: the greener, the farther. One can first see the A* moving in a straight line in the direction of the goal, then when hitting the obstacle, it explores alternative routes through the nodes from the open set.

---

#3: The A* algorithm also has real-world applications. In this example, edges are railroads and h(x) is the great-circle distance (the shortest possible distance on a sphere) to the target. The algorithm is searching for a path between Washington, D.C. and Los Angeles.

 

---

#4: An example of an A* algorithm in action where nodes are cities connected with roads and h(x) is the straight-line distance to target point:

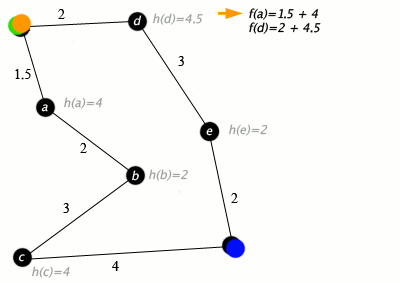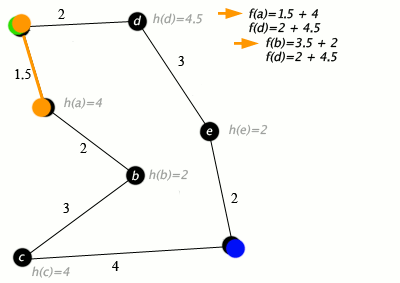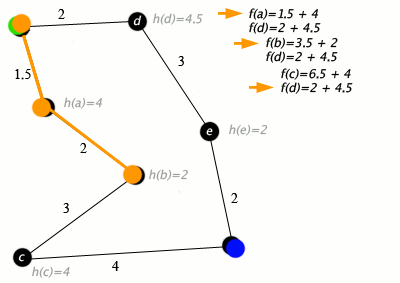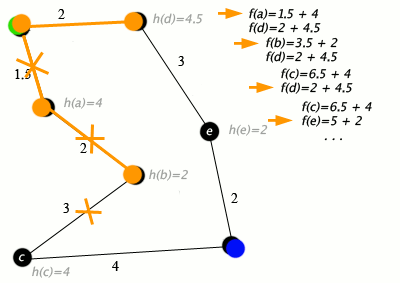
Additional Information (Wikipedia excerpt)

A* was invented by researchers working on Shakey the Robot's path planning.

In 1968, AI researcher Nils Nilsson was trying to improve the path planning done by Shakey the Robot, a prototype robot that could navigate through a room containing obstacles. This path-finding algorithm, which Nilsson called A1, was a faster version of the then best known method, Dijkstra's algorithm, for finding shortest paths in graphs. Bertram Raphael suggested some significant improvements upon this algorithm, calling the revised version A2. Then Peter E. Hart introduced an argument that established A2, with only minor changes, to be the best possible algorithm for finding shortest paths. Hart, Nilsson and Raphael then jointly developed a proof that the revised A2 algorithm was optimal for finding shortest paths under certain well-defined conditions.

A* is an informed search algorithm, or a best-first search, meaning that it solves problems by searching among all possible paths to the solution (goal) for the one that incurs the smallest cost (least distance travelled, shortest time, etc.), and among these paths it first considers the ones that appear to lead most quickly to the solution. It is formulated in terms of weighted graphs: starting from a specific node of a graph, it constructs a tree of paths starting from that node, expanding paths one step at a time, until one of its paths ends at the predetermined goal node.

Example of use in Game design 

Website with files: https://github.com/wordswords/astarpython

Implementation of the A* pathfinding algorithm, with 'Roguelike' text visulisations of the pathfinding in plain ASCII.

Passable squares are denoted by a '0' character, and impassable squares by a '7'. For the sake of simplicity, currently the start square is always the top left square (0,0) and the goal square is always the bottom right square.

Example

This is the board before running:

00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000000777000000000000000
00000000000000000000000000000007777000000000000000
00000000000000077777777777777777700000000000000000
00000000077777777777777777777777700000000000000000
00000077777777777700000000000000000000000000000000
77777777777000000000000000000000000000000000000000
77777777000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
77777777777777777707777777777777777777777777777777
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
70777777777777777777777777777777777777777777777777
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
77777777777777777777700000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000000000777777777777777777777707777777
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000
00000000000000000000700000000000000000000000000000

This is the path found (the '*'s):

**000000000000000000000000000000000000000000000000
0***********************************00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000000777*00000000000000
00000000000000000000000000000007777*00000000000000
00000000000000077777777777777777700*00000000000000
00000000077777777777777777777777700*00000000000000
00000077777777777700000000000000000*00000000000000
77777777777000000000000000000000000*00000000000000
77777777000000000000000000000000000*00000000000000
00000000000000000000000000000000000*00000000000000
00000000000000000000000000000000000*00000000000000
00000000000000000000000000000000000*00000000000000
00000000000000000000000000000000000*00000000000000
00000000000000000000000000000000000*00000000000000
000000000000000000******************00000000000000
777777777777777777*7777777777777777777777777777777
000000000000000000*0000000000000000000000000000000
0******************0000000000000000000000000000000
7*777777777777777777777777777777777777777777777777
0*****************************00000000000000000000
00000000000000000000000000000**0000000000000000000
000000000000000000000000000000**000000000000000000
0000000000000000000000000000000*000000000000000000
0000000000000000000000000000000***0000000000000000
000000000000000000000000000000000*0000000000000000
000000000000000000000000000000000**000000000000000
0000000000000000000000000000000000**00000000000000
77777777777777777777700000000000000***000000000000
0000000000000000000000000000000000000**00000000000
00000000000000000000000000000000000000*00000000000
00000000000000000000000000000000000000**0000000000
000000000000000000000000000000000000000****0000000
000000000000000000007777777777777777777777*7777777
000000000000000000007000000000000000000000**000000
0000000000000000000070000000000000000000000*000000
0000000000000000000070000000000000000000000***0000
000000000000000000007000000000000000000000000**000
0000000000000000000070000000000000000000000000*000
0000000000000000000070000000000000000000000000***0
000000000000000000007000000000000000000000000000*0
000000000000000000007000000000000000000000000000**

Setup

You will need a board to find a path across. Some sample boards are in /boards. Passable squares are denoted by a '0' character, and impassable squares by a '7'. For the sake of simplicity, currently the start square is always the top left square (0,0) and the goal square is always the bottom right square.

Running

python search.py <board txt path> <board width> <board height>

ie:

python search.py boards/board50obs2.txt 50 50

Pseudocode

This was taken from http://en.wikipedia.org/wiki/A*_search_algorithm

More Info

http://www.davidcraddock.net/2014/06/12/a-algorithm-implementation-in-python/