Bubble Sort

Bubble sort is a comparison​-based algorithm that compares each pair of elements in an array and swaps them if they are out of order until the entire array is sorted.

Suggested Video

Challenge

#1 Write a Python program to sort a list of elements using the bubble sort algorithm

#2 Comment each line of the python solution below to show your understanding of the algorithm

Try it yourself

Solution

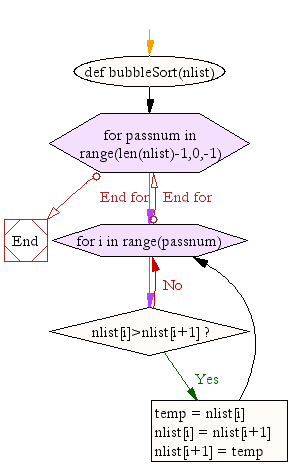
def bubbleSort(nlist):
    for passnum in range(len(nlist)-1,0,-1):
        for i in range(passnum):
            if nlist[i]>nlist[i+1]:
                temp = nlist[i]
                nlist[i] = nlist[i+1]
                nlist[i+1] = temp

nlist = [14,46,43,27,57,41,45,21,70]
bubbleSort(nlist)
print(nlist)

Animated Demo

---

---

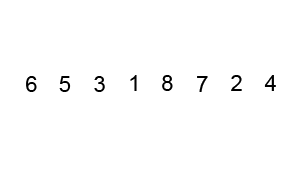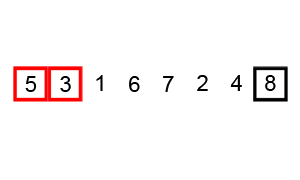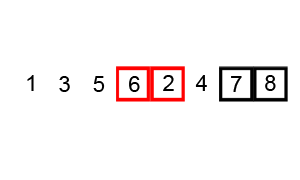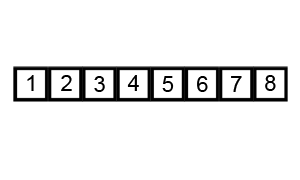
Flowchart

Additional Information (Wikipedia excerpt)

For each element in the list, the algorithm compares every pair of elements."Bubble sort, sometimes referred to as sinking sort, is a relatively and comparitively simple sorting algorithm that repeatedly steps through the list to be sorted, compares each pair of adjacent items and swaps them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm, which is a comparison sort, is named for the way smaller elements "bubble" to the top of the list, hence the name! Although the algorithm is simple, it is too slow and impractical for most problems even when compared to insertion sort. It can be practical if the input is usually in sort order but may occasionally have some out-of-order elements nearly in position. 

An example of bubble sort.

Starting from the beginning of the list, compare every adjacent pair, swap their position if they are not in the right order (the latter one is smaller than the former one). After each iteration, one less element (the last one) is needed to be compared until there are no more elements left to be compared.

Performance

Bubble sort has worst-case and average complexity both О(n²), where n is the number of items being sorted. There exist many sorting algorithms, such as merge sort with substantially better worst-case or average complexity of O(n log n). Even other О(n²) sorting algorithms, such as insertion sort, tend to have better performance than bubble sort. Therefore, bubble sort is not a practical sorting algorithm when n is large.

The only significant advantage that bubble sort has over most other implementations, even quicksort, but not insertion sort, is that the ability to detect that the list is sorted efficiently is built into the algorithm. When the list is already sorted (best-case), the complexity of bubble sort is only O(n). By contrast, most other algorithms, even those with better average-case complexity, perform their entire sorting process on the set and thus are more complex. However, not only does insertion sort have this mechanism too, but it also performs better on a list that is substantially sorted (having a small number of inversions).

Bubble sort should be avoided in the case of large collections. It will not be efficient in the case of a reverse-ordered collection.

Rabbits and turtles

The distance and direction that elements must move during the sort determine bubble sort's performance because elements move in different directions at different speeds. An element that must move toward the end of the list can move quickly because it can take part in successive swaps. For example, the largest element in the list will win every swap, so it moves to its sorted position on the first pass even if it starts near the beginning. On the other hand, an element that must move toward the beginning of the list cannot move faster than one step per pass, so elements move toward the beginning very slowly. If the smallest element is at the end of the list, it will take n−1 passes to move it to the beginning. This has led to these types of elements being named rabbits and turtles, respectively, after the characters in Aesop's fable of The Tortoise and the Hare.

Various efforts have been made to eliminate turtles to improve upon the speed of bubble sort. Cocktail sort is a bi-directional bubble sort that goes from beginning to end, and then reverses itself, going end to beginning. It can move turtles fairly well, but it retains O(n²) worst-case complexity. Comb sort compares elements separated by large gaps, and can move turtles extremely quickly before proceeding to smaller and smaller gaps to smooth out the list. Its average speed is comparable to faster algorithms like quicksort.

Step-by-step example

Let us take the array of numbers "5 1 4 2 8", and sort the array from lowest number to greatest number using bubble sort. In each step, elements written in bold are being compared. Three passes will be required.

Example:
First Pass:
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1.
( 1 5 4 2 8 ) –>  ( 1 4 5 2 8 ), Swap since 5 > 4
( 1 4 5 2 8 ) –>  ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.

Second Pass:
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –>  ( 1 2 4 5 8 )
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without anyswap to know it is sorted.

Third Pass:
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

Implementation

Pseudocode implementation

The algorithm can be expressed as (0-based array):

procedure bubbleSort( A : list of sortable items )
    n = length(A)
    repeat 
        swapped = false
        for i = 1 to n-1 inclusive do
            /* if this pair is out of order */
            if A[i-1] > A[i] then
                /* swap them and remember something changed */
                swap( A[i-1], A[i] )
                swapped = true
            end if
        end for
    until not swapped
end procedure