Binary Search

A binary search algorithm takes the data and keeps dividing it in half until it finds the item it is looking for.

Suggested Video

How to code a Binary search - step by step

A step by step explanation of how to code a Binary search in python using a relevant example: searching a friend list (e.g. facebook) for a friend!

Challenge

#1 Write a Python program to search using the binary search method

#2 Comment each line of the python solution below to show your understanding of the algorithm

Try it yourself

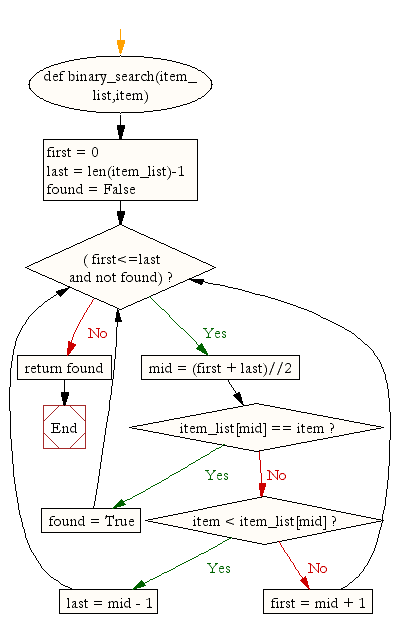
Solution

def binary_search(item_list,item):
	first = 0
	last = len(item_list)-1
	found = False
	while( first<=last and not found):
		mid = (first + last)//2
		if item_list[mid] == item :
			found = True
		else:
			if item < item_list[mid]:
				last = mid - 1
			else:
				first = mid + 1	
	return found
	
print(binary_search([1,2,3,5,8], 6))
print(binary_search([1,2,3,5,8], 5))

Explanation with Example

---

Imagine that you have a database of customers and want to search for the customer John Smith. We first need the database to be ordered into alphabetical order by surname. We then search for the record ‘John Smith’ by surname.

The binary search will split the database in half, and compare the midpoint (the middle name) to the name ‘John Smith’. It will see whether the midpoint comes before or after ‘Smith’ and will throw away the set of records that doesn’t contain ‘Smith’ as a surname. It will keep dividing the records in that way until it reaches two records left, one of which is ‘John Smith’. It will then throw away the other record and output John Smith’s details. Binary search effectively divides the data in half and throws away, or ‘bins’ the half that does not contain the search term. (Source: BBC Bitesize)

---

Above example represented as a flow chart 

In pseudocode this would look like:

OUTPUT "Which customer do you want to find?"
INPUT user inputs John Smith
STORE the user's input in the customer_name variable
customer_found = False
(we need to create a flag that identifies if the customer is found)
WHILE customer_found = False:
	Find midpoint of list
	IF customer_name = record at midpoint of list THEN
		customer_found = True
	ELSE IF customer comes before the midpoint THEN
		throw away the second half of the list
	ELSE 
		throw away the first part of the list
OUTPUT customer details

General Flow Chart

Additional Information (Wikipedia excerpt)

In computer science, binary search, also known as half-interval search, logarithmic search,or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array; if they are unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful. If the search ends with the remaining half being empty, the target is not in the array.

Binary search runs in at worst logarithmic time, making O(log n) comparisons, where n is the number of elements in the array, the O is Big O notation, and log is the logarithm. Binary search takes constant (O(1)) space, meaning that the space taken by the algorithm is the same for any number of elements in the array. Although specialized data structures designed for fast searching—such as hash tables—can be searched more efficiently, binary search applies to a wider range of problems.

Although the idea is simple, implementing binary search correctly requires attention to some subtleties about its exit conditions and midpoint calculation.

There are numerous variations of binary search. In particular, fractional cascading speeds up binary searches for the same value in multiple arrays, efficiently solving a series of search problems in computational geometry and numerous other fields. Exponential search extends binary search to unbounded lists. The binary search tree and B-tree data structures are based on binary search.

Interesting facts and History

In 1946, John Mauchly made the first mention of binary search as part of the Moore School Lectures, the first ever set of lectures regarding any computer-related topic.Every published binary search algorithm worked only for arrays whose length is one less than a power of two until 1960, when Derrick Henry Lehmer published a binary search algorithm that worked on all arrays. In 1962, Hermann Bottenbruch presented an ALGOL 60 implementation of binary search that placed the comparison for equality at the end, increasing the average number of iterations by one, but reducing to one the number of comparisons per iteration.The uniform binary search was presented to Donald Knuth in 1971 by A. K. Chandra of Stanford University and published in Knuth's The Art of Computer Programming. In 1986, Bernard Chazelle and Leonidas J. Guibas introduced fractional cascading as a method to solve numerous search problems in computational geometry

Library Support

Many languages' standard libraries include binary search routines:

• C provides the function bsearch() in its standard library, which is typically implemented via binary search (although the official standard does not require it so)
• C++'s Standard Template Library provides the functions binary_search(), lower_bound(), upper_bound() and equal_range().
• COBOL provides the SEARCH ALL verb for performing binary searches on COBOL ordered tables
• Java offers a set of overloaded binarySearch() static methods in the classes Arrays and Collections in the standard java.util package for performing binary searches on Java arrays and on Lists, respectively.
• Microsoft's .NET Framework 2.0 offers static generic versions of the binary search algorithm in its collection base classes. An example would be System.Array's method BinarySearch<T>(T[] array, T value).
• Python provides the bisect module.
• Ruby's Array class includes a bsearch method with built-in approximate matching.
• Go's sort standard library package contains the functions Search, SearchInts, SearchFloat64s, and SearchStrings, which implement general binary search, as well as specific implementations for searching slices of integers, floating-point numbers, and strings, respectively.
• For Objective-C, the Cocoa framework provides the NSArray -indexOfObject:inSortedRange:options:usingComparator: method in Mac OS X 10.6+. Apple's Core Foundation C framework also contains a CFArrayBSearchValues() function