Merge Sort

Mergesort is another comparison-based algorithm also known as a "divide and conquer" algorithm and its main focus is on how to merge together two pre-sorted arrays such that the resulting array is also sorted. You may be interested to know that it was invented by the marvellous John von Neumann in 1945.

The key word of course is 'merge', so we are referring to bringing two lists together. Conceptually, a merge sort works as follows : First, divide the unsorted list into n sublists, each containing 1 element (a list of 1 element is considered sorted). Then, repeatedly merge sub lists to produce new sorted sublists until there is only 1 sublist remaining. This will be the sorted list.

Suggested Video

>

Challenge

#1 Write a Python program to sort a list of elements using the Merge sort algorithm

#2 Comment each line of the python solution below to show your understanding of the algorithm

Try it yourself

Solution

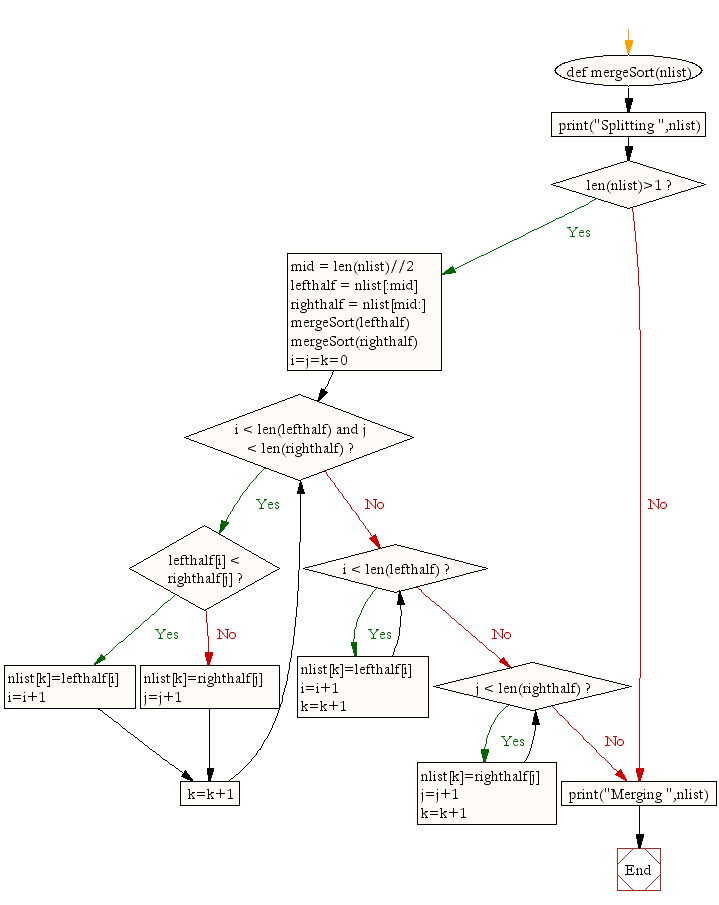
def mergeSort(nlist):
    print("Splitting ",nlist)
    if len(nlist)>1:
        mid = len(nlist)//2
        lefthalf = nlist[:mid]
        righthalf = nlist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)
        i=j=k=0       
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                nlist[k]=lefthalf[i]
                i=i+1
            else:
                nlist[k]=righthalf[j]
                j=j+1
            k=k+1

        while i < len(lefthalf):
            nlist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j < len(righthalf):
            nlist[k]=righthalf[j]
            j=j+1
            k=k+1
    print("Merging ",nlist)

nlist = [14,46,43,27,57,41,45,21,70]
mergeSort(nlist)
print(nlist)

Animated Demo

---

---

Flow Chart

Additional Information

A recursive merge sort algorithm used to sort an array of 7 integer values. These are the steps a human would take to emulate merge sort (top-down).

In sorting n objects, merge sort has an average and worst-case performance of O(n log n). If the running time of merge sort for a list of length n is T(n), then the recurrence T(n) = 2T(n/2) + n follows from the definition of the algorithm (apply the algorithm to two lists of half the size of the original list, and add the n steps taken to merge the resulting two lists). The closed form follows from the master theorem for divide-and-conquer recurrences.

In the worst case, the number of comparisons merge sort makes is equal to or slightly smaller than (n ⌈lg n⌉ - 2^⌈lg n⌉ + 1), which is between (n lg n - n + 1) and (n lg n + n + O(lg n)).

For large n and a randomly ordered input list, merge sort's expected (average) number of comparisons approaches α·n fewer than the worst case where {\displaystyle \alpha =-1+\sum _{k=0}^{\infty }{\frac {1}{2^{k}+1}}\approx 0.2645.}

Comparisons

In the worst case, merge sort does about 39% fewer comparisons than quicksort does in the average case. In terms of moves, merge sort's worst case complexity is O(n log n)—the same complexity as quicksort's best case, and merge sort's best case takes about half as many iterations as the worst case.

Merge sort is more efficient than quicksort for some types of lists if the data to be sorted can only be efficiently accessed sequentially, and is thus popular in languages such as Lisp, where sequentially accessed data structures are very common. Unlike some (efficient) implementations of quicksort, merge sort is a stable sort.

Merge sort's most common implementation does not sort in place; therefore, the memory size of the input must be allocated for the sorted output to be stored in (see below for versions that need only n/2 extra spaces).

Although heapsort has the same time bounds as merge sort, it requires only Θ(1) auxiliary space instead of merge sort's Θ(n). On typical modern architectures, efficient quicksort implementations generally outperform mergesort for sorting RAM-based arrays.^{[citation needed]}On the other hand, merge sort is a stable sort and is more efficient at handling slow-to-access sequential media. Merge sort is often the best choice for sorting a linked list: in this situation it is relatively easy to implement a merge sort in such a way that it requires only Θ(1) extra space, and the slow random-access performance of a linked list makes some other algorithms (such as quicksort) perform poorly, and others (such as heapsort) completely impossible.

As of Perl 5.8, merge sort is its default sorting algorithm (it was quicksort in previous versions of Perl). In Java, the Arrays.sort() methods use merge sort or a tuned quicksort depending on the datatypes and for implementation efficiency switch to insertion sort when fewer than seven array elements are being sorted. The Linux kernel uses merge sort for its linked lists.Python uses Timsort, another tuned hybrid of merge sort and insertion sort, that has become the standard sort algorithm in Java SE 7, on the Android platform, and in GNU Octave

External links

• Animated Sorting Algorithms: Merge Sort at the Wayback Machine (archived 6 March 2015) – graphical demonstration
• Dictionary of Algorithms and Data Structures: Merge sort
• Mergesort applet with "level-order" recursive calls to help improve algorithm analysis
• Open Data Structures - Section 11.1.1 - Merge Sort