Learn. Test. Track.
TestandTrack.io -the all in one platform for computer science, programming and ICT. Integrated resources, analytics, tracking, personalised feedback and self marking tests. All topics, all done for you.
Join 36,000+ teachers and students using TTIO.

Assessment, learning, tracking and feedback all sorted!
All in one platform for Computer Science, ICT and Programming. Integrated resources (ppts, tutorials, videos) and self marking tests. All trackable with class analytics and even personalised individual feedback. Assessment, grade book and tracking, all done for you!
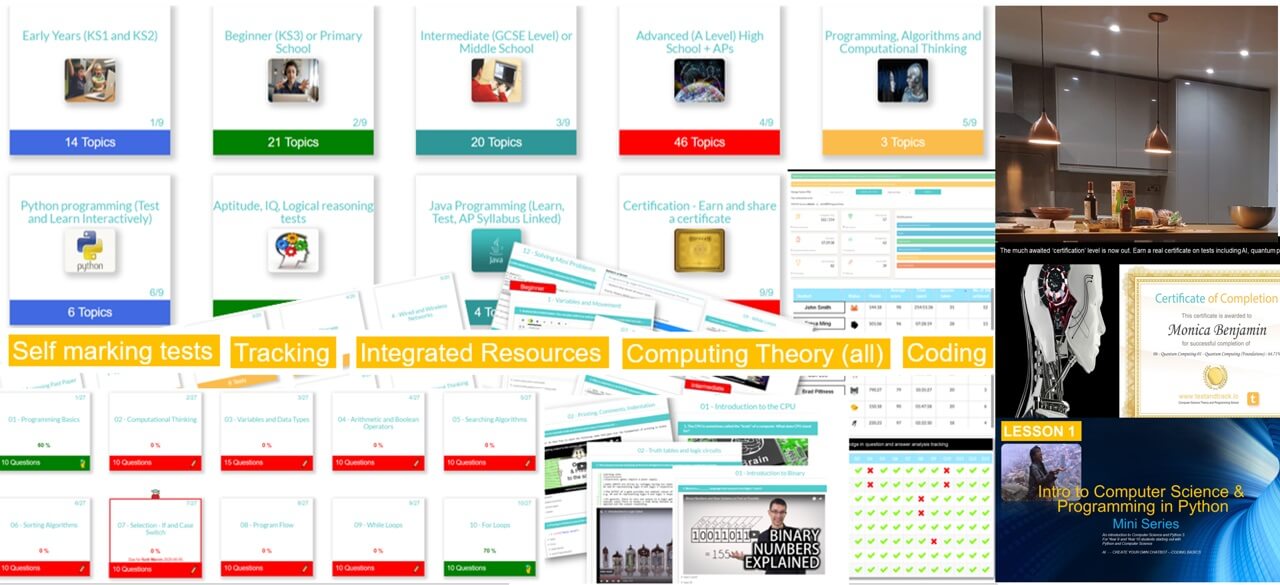
Content and Features
All years, all covered, everything done for you! Topical - tailored to computer science and programming curriculum.
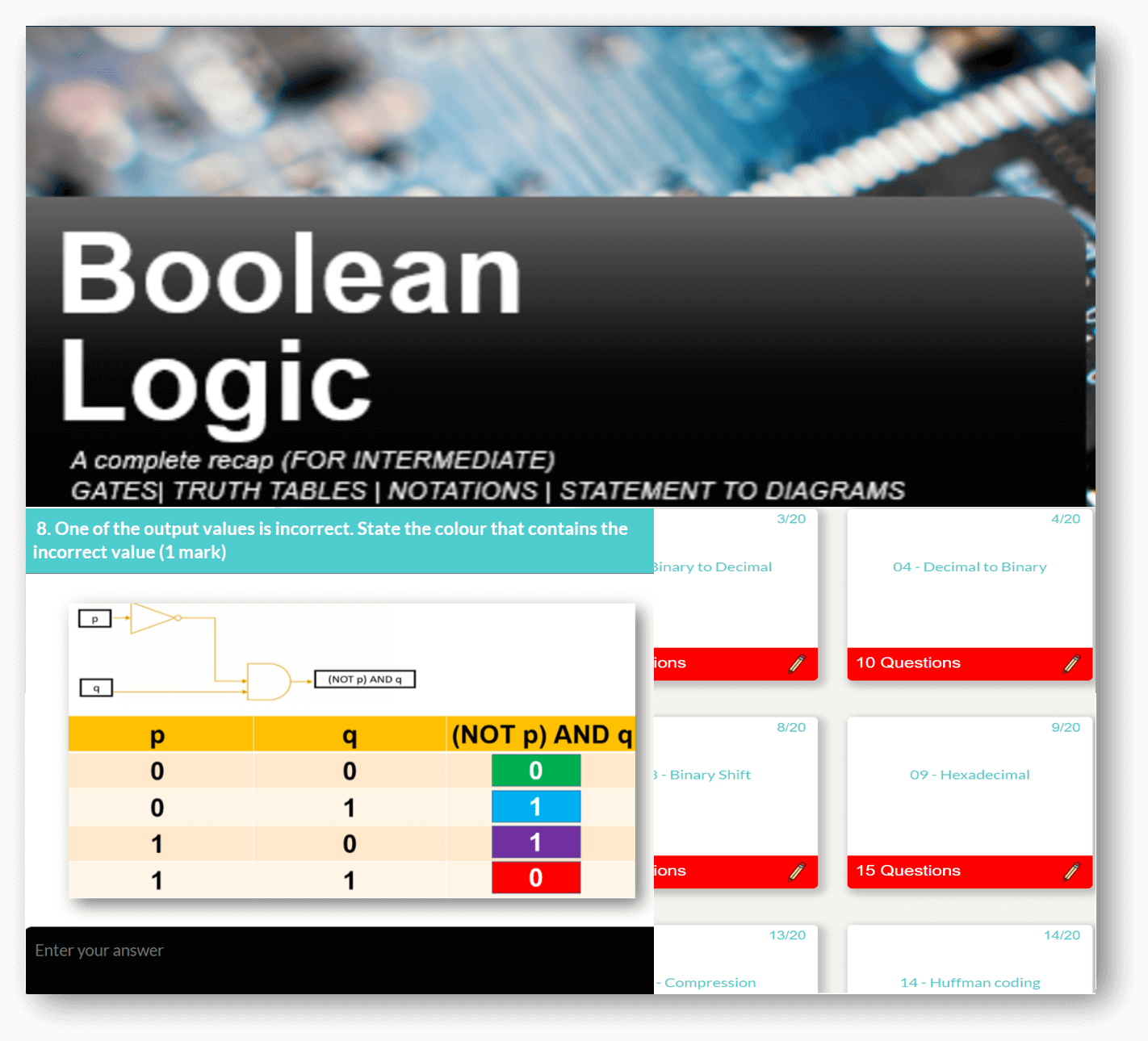
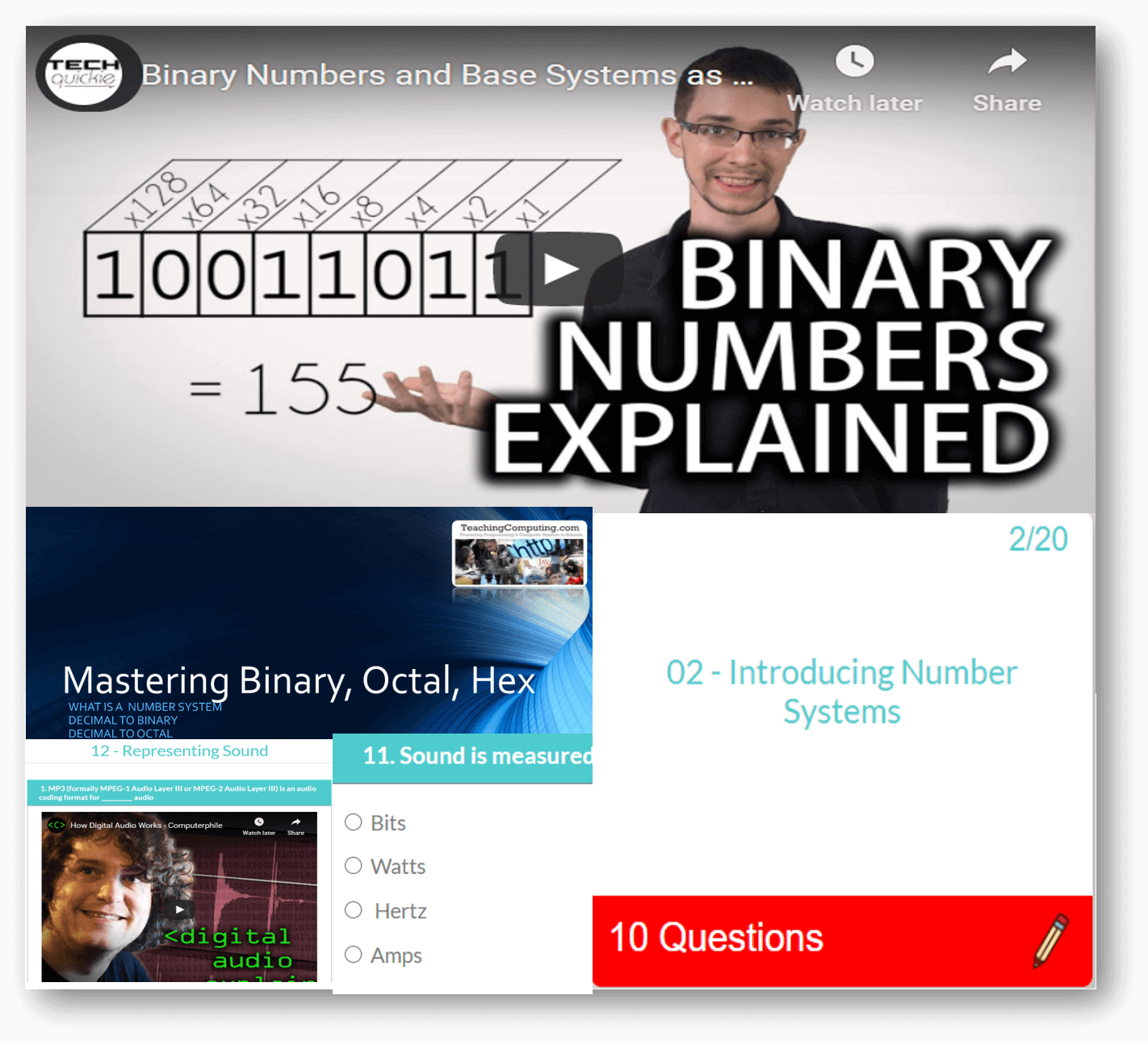
Computer Science theory like CPU, Networks through to Data Representation and Boolean Logic.
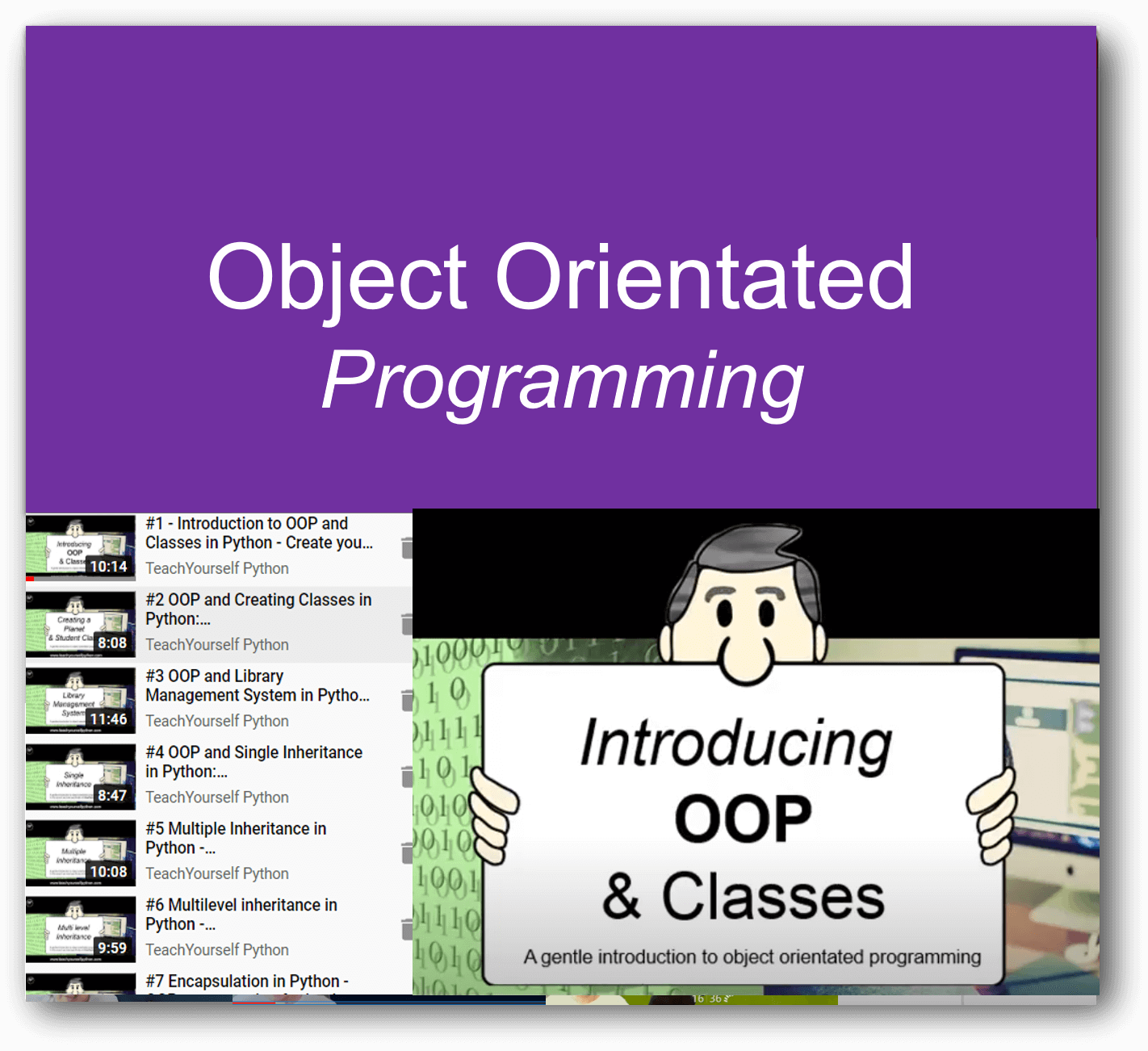
Programming pathways: The perfect way to get started with coding. Beginner through to advanced, including highly recommended series on Flask, Web scraping and more.
Why TestandTrack?
There are plenty of platforms which have resources, or standalone quizzes, but TestandTrack has both! Not only that but together with awesome class analytics, personalised automated feedback and a ton of tracking of features, your assessment is sorted with more time to focus on teaching and inspiring students to learn.
Integrated resources
Most of our tests have integrated resources in the form of videos, powerpoints or tutorials (for programming pathways). Set tasks using our resources, or there is also the option to provide external links for further study.
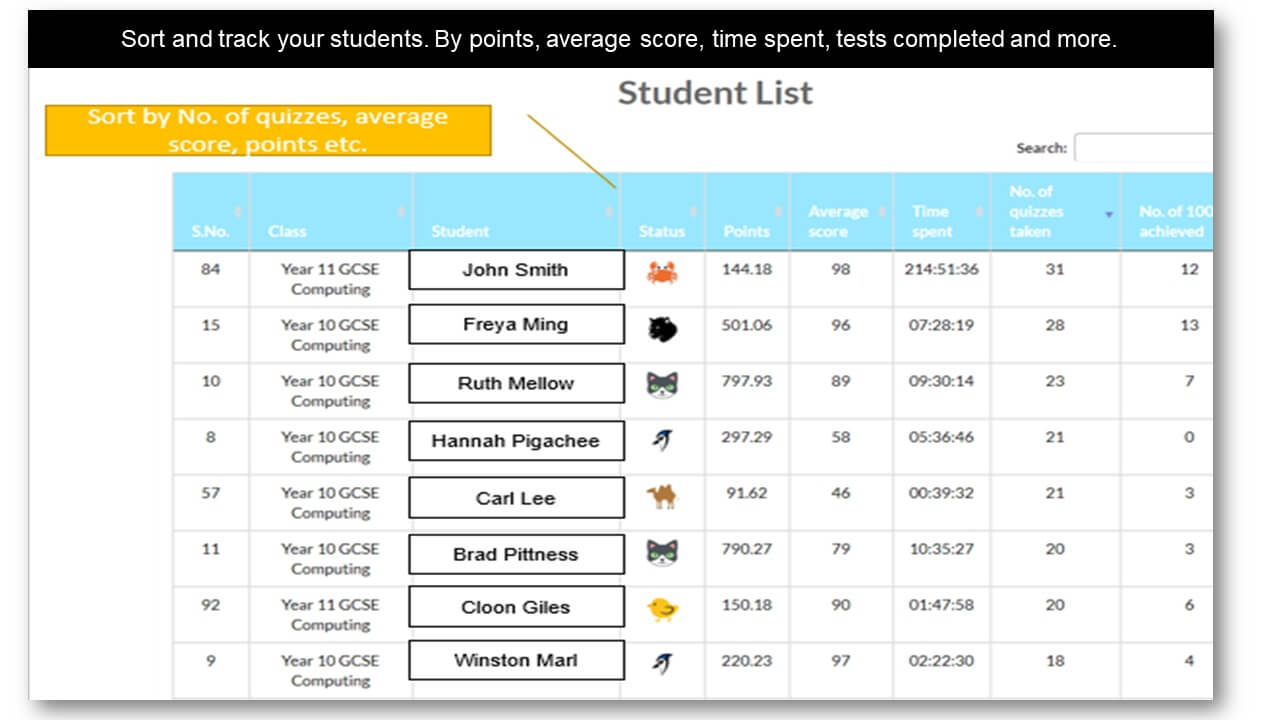
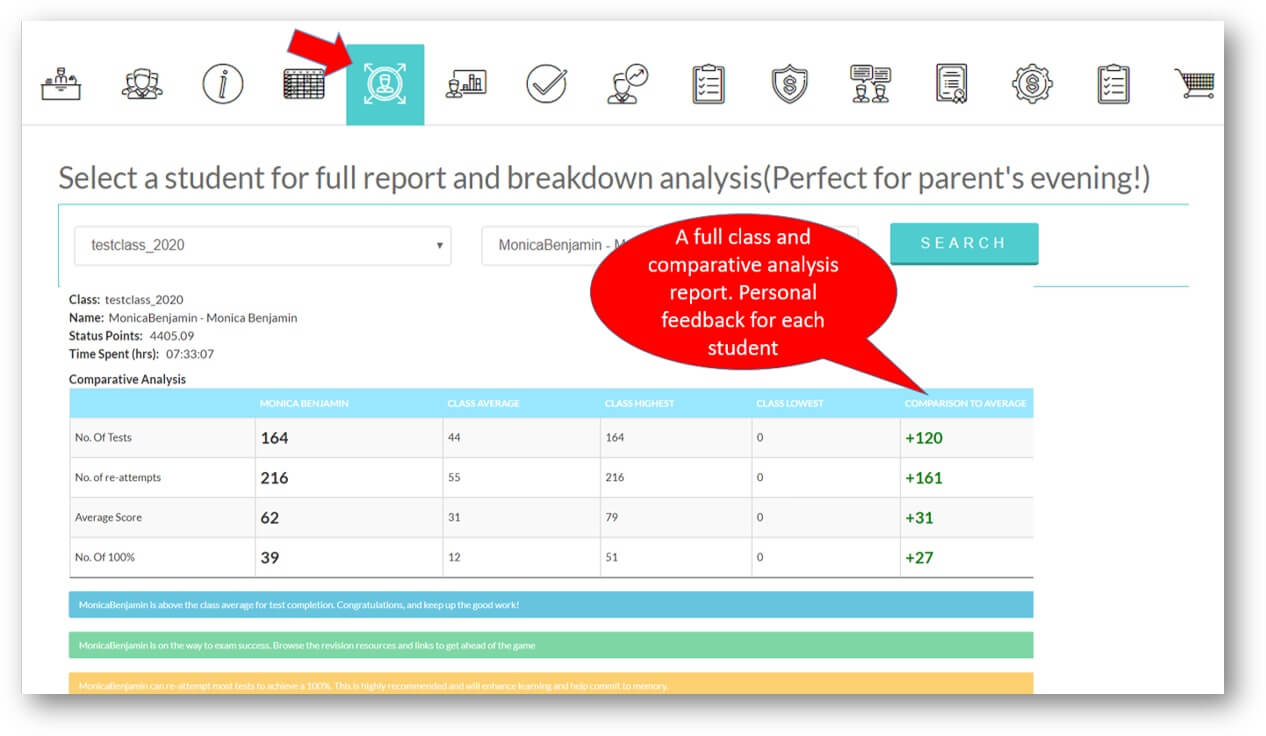
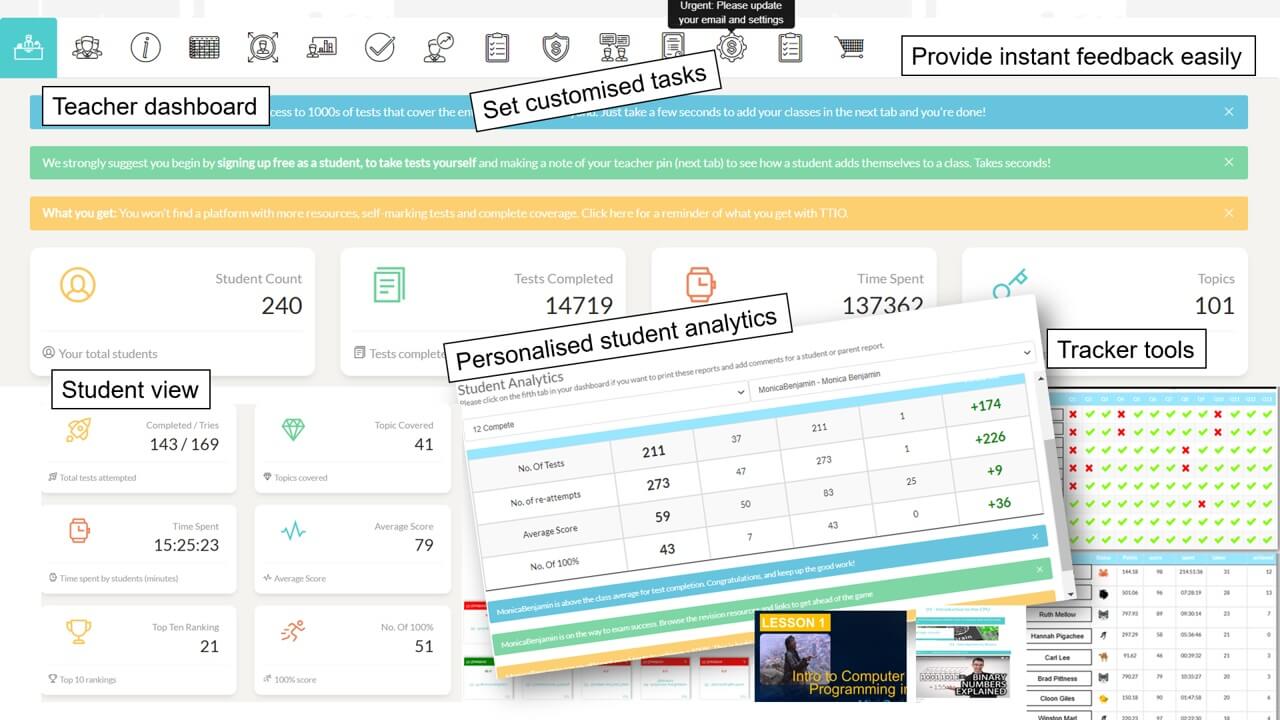
Analytics and Tracking
Each student receives automatic and specific feedback giving them the impetus to improve/compete. Comprehensive teacher tracking tools. Engagement with status points, rankings, leaderboards, re-attempts and more.
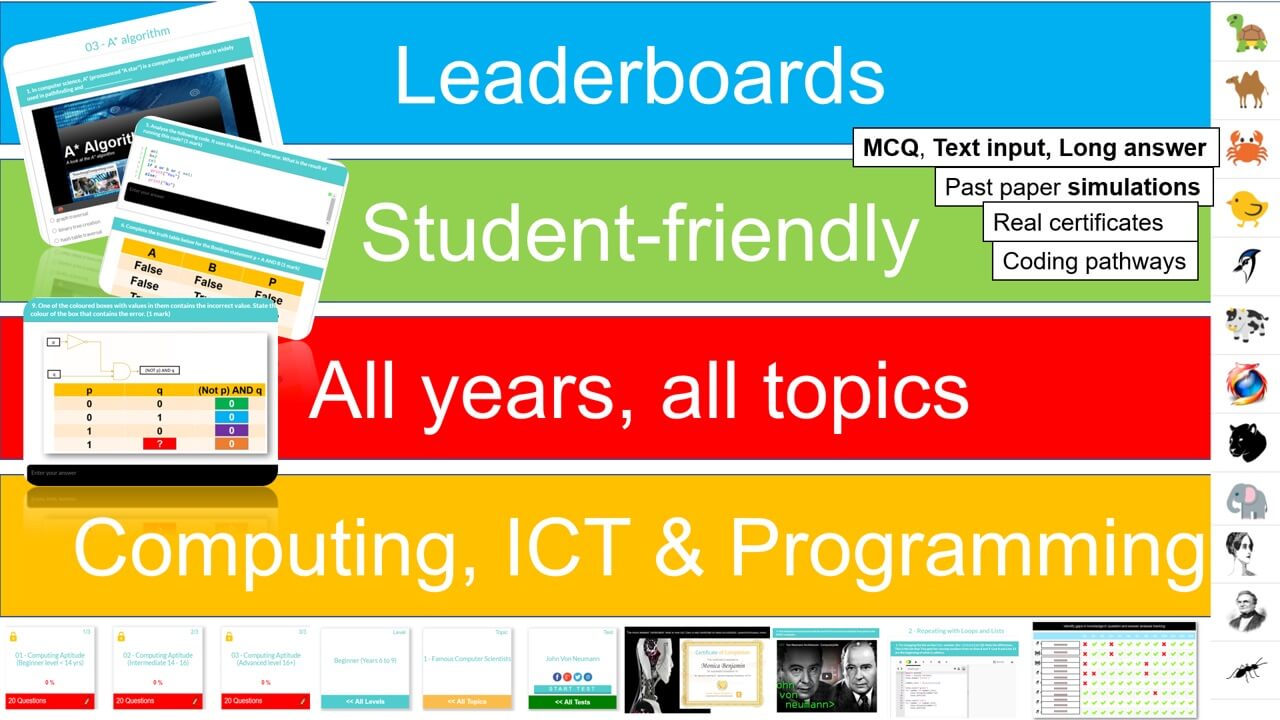
CS, ICT and Programming
We cover all syllabus topics: Early years to Advanced. More content than any other platform, self-marking tests, MCQ and text entry. CS theory, ICT and Programming. See them go to zero to pro in just five of our integrated coding lessons.
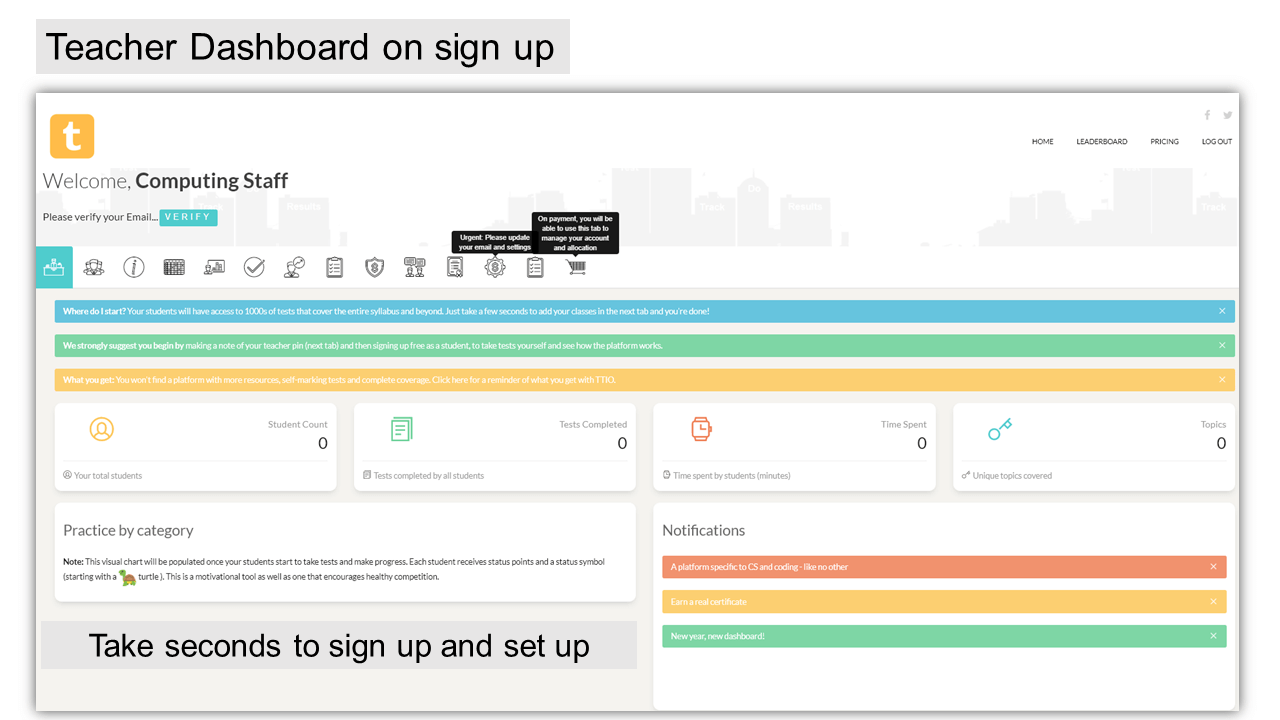
Seconds to set up and sign up
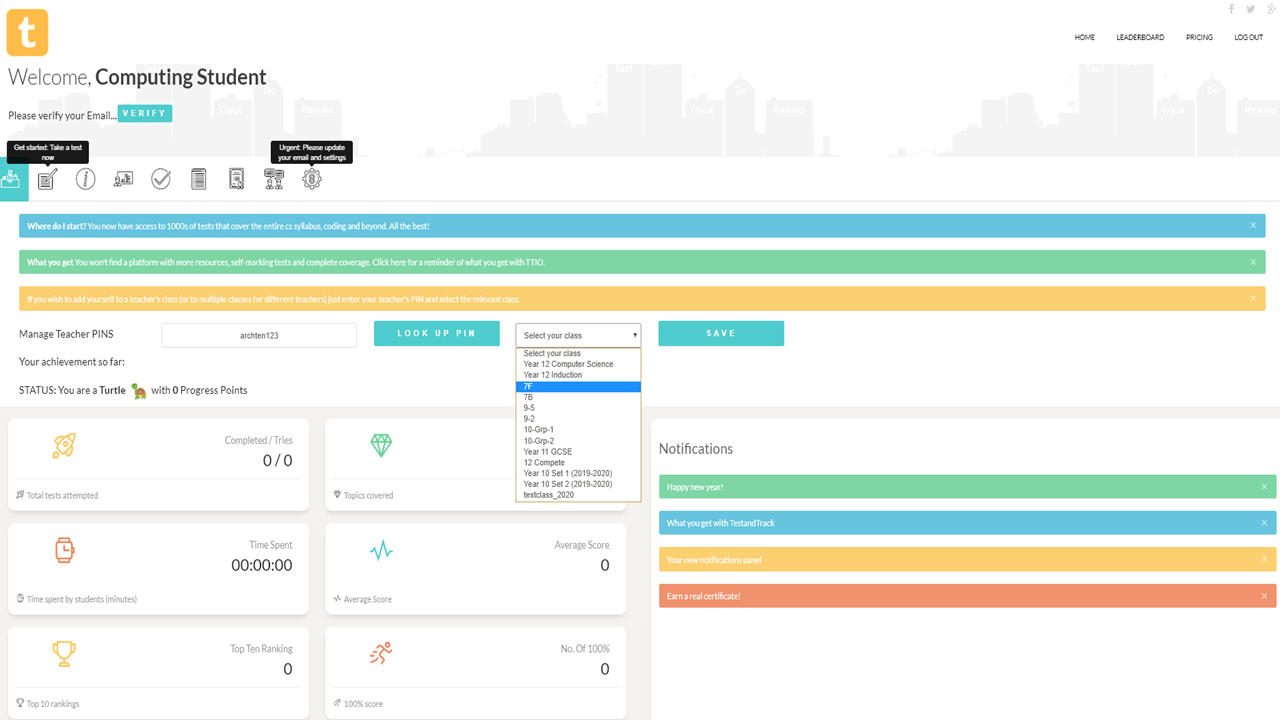
1. Sign up as a teacher. 2. Enter a teacher PIN. 3. Add class names 4. Give your teacher PIN to students. 5. Once students start taking tests, your tracking starts.

See flipped learning at its best
743
Time spent (mins)
394
No. of Tests
93%
Average Score
Testimonials
Learning is for everyone and that's what TestandTrack is about. We've done all the leg work for you so teachers can focus on teaching and students can learn.
I would genuinely like to thank you TestandTrack team because I would never have achieved my top grade and ability to code in python without you. I enjoyed learning, competing and seeing my progress.
There is nothing quite like TestandTrack out there. In just the first week, my students had completed a total of 450 tests! Tracking, grading and feedback sorted!
I loved the competitive element and personalised class-based feedback and ranking. I also loved being able to go further and get ahead of the syllabus, for instance the web scraping series was awesome - I did it with my Dad.
For the sheer wealth of resources, tests and tracking TTIO is ridiculously amazing value for money. I use TestandTrack with all my classes. It saves me hours of planning and is flipped learning at its best.
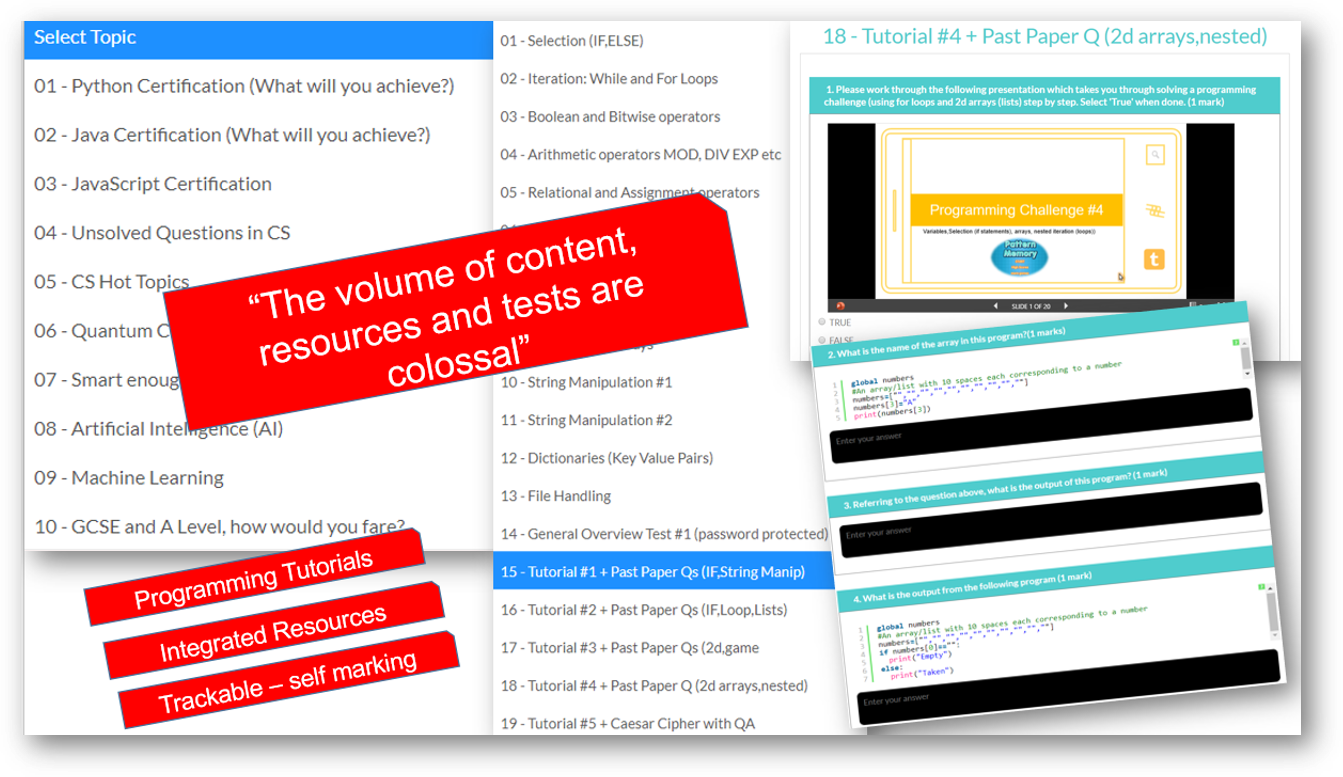
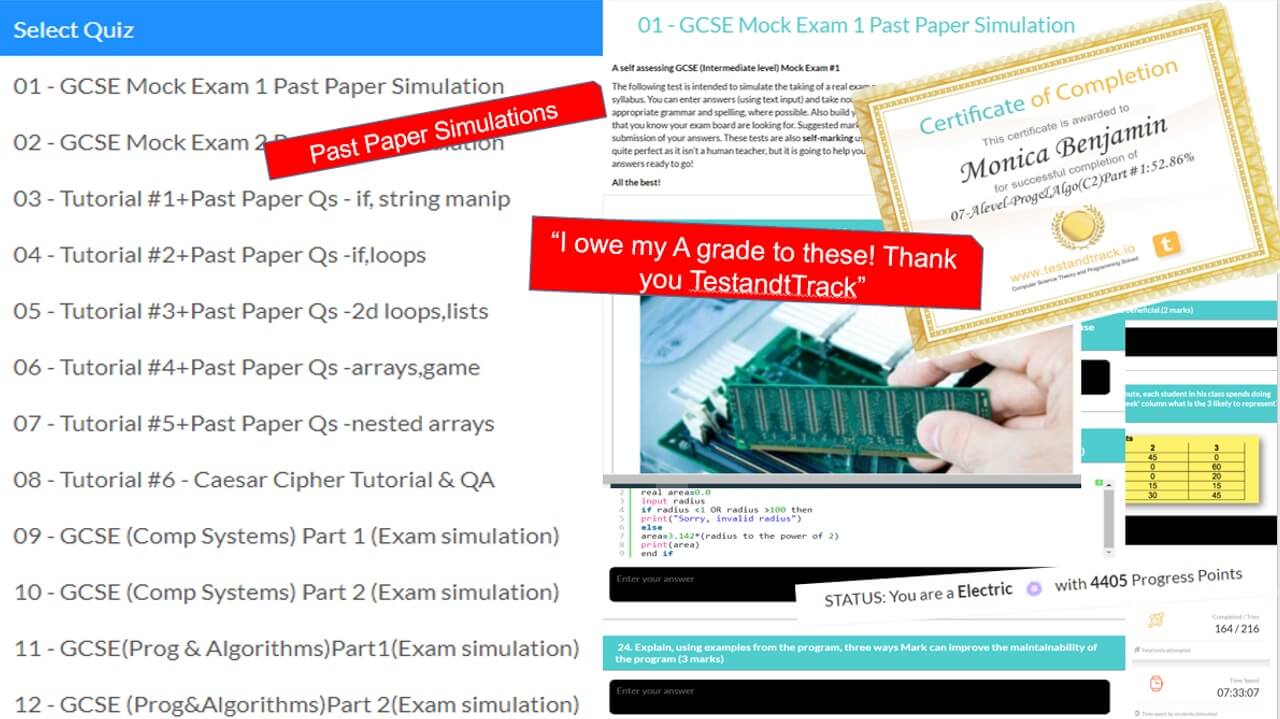
Preview: Levels, Topics, Resources and Tests
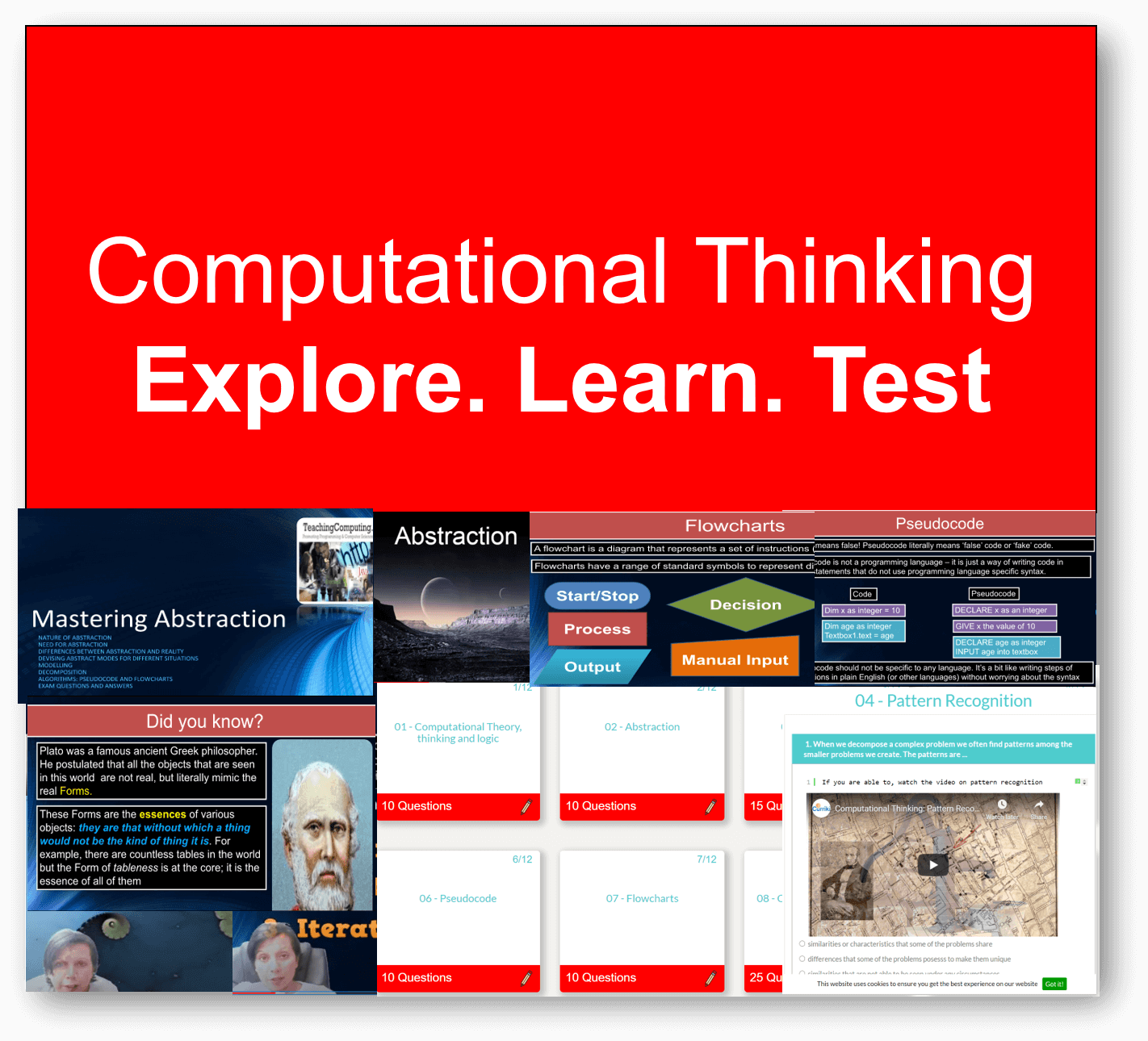
All years. All levels. Comprehensive syllabus coverage. There are literally thousands of tests, resources and comprehensive topical coverage for all of computer science theory, ICT and programming. Have a quick preview by clicking below. Teachers: You can set specific topics, or tests for students to complete, use our resources for learning, or provide an external link to your own. Furthermore, you can even set your own assignments or questions.









Featured Series
For absolute beginner's right through to advanced, we have something for all of you. Check out some of our popular series below, and on sign up, there is so much more!
Contact us
Our Location
Caterham, South London
United Kingdom
Working Hours
Mon - Fri: 8:30am - 7:30pm
Want to see something on testandtrack? Pleased? Have an idea? Do drop us a line, we'd love to hear from you.
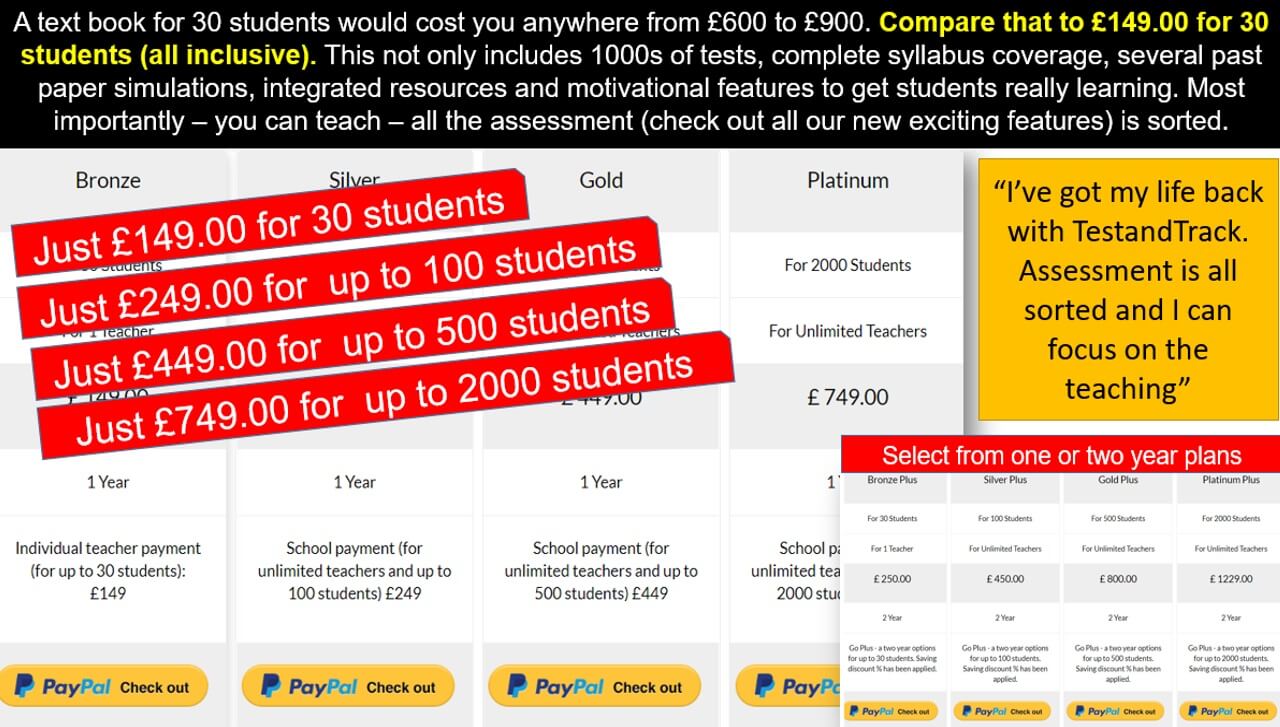
Get started with your Free Trial!
There is no obligation, but once you've tried TestandTrack, we hope you won't look back. Do trial the platform and use all its features.